In 2009 the Mandelbulb became the fractal of the year in some informal way, it became really popular. I was one of the people that pioneered a bit the field in terms of optimizations and rendering shadows for it, but the original idea of the fractal itself wasn't mine at all. Here is below what I wrote back then, and a video I made soon after:
A Mandelbulb fractal rendered in realtime over mobile phone footage
The idea of the Mandelbulb fractal came to be through yet another attempt at creating a 3D fractal that is as iconic as the traditional 2D Mandelbrot set is. Unlike 4D Julia sets which naturally arise from simply generalizing the 2D complex Julia sets to quaternions, all efforts to produce an universal and intersting 4D Mandelbrot set been futile, and to this day (2020) nobody has found a satisfactory fractal. But, the Mandelbulb was one of those attempts.
While usually Quaternions, hypercomplex numbers and all other sort of (often inconsistent) algebras had been used in previous attempts, the construction of the Mandelbulb takes a different approach. Instead of thinking in algebra and in the usual iteration formula w->w^2+c, this time we think on the classic 2D set as the result of a geometric process of iterating points by squaring their distance to the origin, rotating them by an angle equal to the current angle with the positive x axis, and then translating by c. Now it's possible to try to extend this geometric process to three dimensions regardless of any algebraic correctness. And in fact the Mandelbulb formula is completely wrong and incoherent in terms its algebra, but it produces beautiful images, which is in itself a sign that, perhaps, algebraic correctness is not what we always want. In fact, most of the proto-Mandelbulb images shown in the forums were produced with buggy code that implemented the geometric transformations completely wrong, with incorrect derivatives calculation for the distance estimation, etc, yet the images were looking just right. The lesson learnt with this is that there is something about duplicating lengths and angles that for some reason makes sense, not only regardless of algebraic correctness of meaning, but even regardless of any geometric interpretation. This idea is reinforced by the fact that when breaking the rule of equal length exponentiation to equal angle multiplication, the structure of the set is broken.
Because in the end any formula that follows the equal-length-exponentiation-to-equal-angle-multiplication will do, I will choose the one that is geometrically correct, unlike what's documented elsewhere. If you are unsure if the code you read in other forums or websites is correct, follow the one here.
The basic formulation of the Mandelbulb is derived from extracting the polar coordinates of a 3D point and doubling its angles and squaring its length. The idea of duplicating can be generalized to triplicating, or more popularly multiplying by eight. We will in fact choose the arbitrary value of eight, because for higher powers the asymptotic behaviour of the formulas tends to produce more symmetric shapes. So, let's call w to our 3D point, then choose eight as our polynomial degree for our Mandelbrot, and so multiply the polar angles of our 3D point by eight and expand it's modulo by a power of eight:
We only have to add c to w now and iterate it in the regular way. You can pretty much then take the code and insert it in your favourite raymarching engine (like this very old but simple one), unless you care about rendering speed.

The above code is mathematically correct, and even fast enough to run in realtime in modern hardware. However, one can still gain a 5x speed factor when rendering in some cases (like when rendering in the CPU in pure C or C++).
The first thing to do is, as usual, to get rid of all those transcendental functions (the trigonometric ones) which not only are slow but also introduce unnecessary errors in the computations. By using the basic trigonometric identities of the cosine and sine of a doubled angle, one can replace the 8-times angle computations by repeatedly applying the identities (three times). The result is a polynomial which has no trigonometric functions and runs much faster in the most CPUs (but not in GPUs usually, which have super fast trigonometric implementations):
You can find a realtime implementation of this here: https://www.shadertoy.com/view/ltfSWn
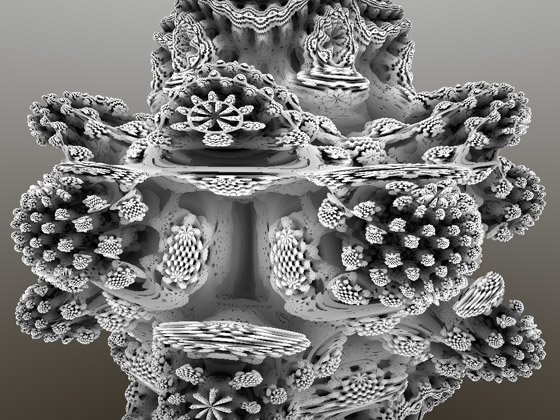
Orbit trap for coloring. Note that there are no lighting computations of any sort going on
The first video is a close zoom to the surface of the fractal object, and the second one is a morphing of the associated Julia sets of the Mandelbulb set.
The idea
The idea of the Mandelbulb fractal came to be through yet another attempt at creating a 3D fractal that is as iconic as the traditional 2D Mandelbrot set is. Unlike 4D Julia sets which naturally arise from simply generalizing the 2D complex Julia sets to quaternions, all efforts to produce an universal and intersting 4D Mandelbrot set been futile, and to this day (2020) nobody has found a satisfactory fractal. But, the Mandelbulb was one of those attempts.
While usually Quaternions, hypercomplex numbers and all other sort of (often inconsistent) algebras had been used in previous attempts, the construction of the Mandelbulb takes a different approach. Instead of thinking in algebra and in the usual iteration formula w->w^2+c, this time we think on the classic 2D set as the result of a geometric process of iterating points by squaring their distance to the origin, rotating them by an angle equal to the current angle with the positive x axis, and then translating by c. Now it's possible to try to extend this geometric process to three dimensions regardless of any algebraic correctness. And in fact the Mandelbulb formula is completely wrong and incoherent in terms its algebra, but it produces beautiful images, which is in itself a sign that, perhaps, algebraic correctness is not what we always want. In fact, most of the proto-Mandelbulb images shown in the forums were produced with buggy code that implemented the geometric transformations completely wrong, with incorrect derivatives calculation for the distance estimation, etc, yet the images were looking just right. The lesson learnt with this is that there is something about duplicating lengths and angles that for some reason makes sense, not only regardless of algebraic correctness of meaning, but even regardless of any geometric interpretation. This idea is reinforced by the fact that when breaking the rule of equal length exponentiation to equal angle multiplication, the structure of the set is broken.
The algorithm
Because in the end any formula that follows the equal-length-exponentiation-to-equal-angle-multiplication will do, I will choose the one that is geometrically correct, unlike what's documented elsewhere. If you are unsure if the code you read in other forums or websites is correct, follow the one here.
The basic formulation of the Mandelbulb is derived from extracting the polar coordinates of a 3D point and doubling its angles and squaring its length. The idea of duplicating can be generalized to triplicating, or more popularly multiplying by eight. We will in fact choose the arbitrary value of eight, because for higher powers the asymptotic behaviour of the formulas tends to produce more symmetric shapes. So, let's call w to our 3D point, then choose eight as our polynomial degree for our Mandelbrot, and so multiply the polar angles of our 3D point by eight and expand it's modulo by a power of eight:
// extract polar coordinates
float wr = sqrt(dot(w,w));
float wo = acos(w.y/wr);
float wi = atan(w.x,w.z);
// scale and rotate the point
wr = pow( wr, 8.0 );"
wo = wo * 8.0;"
wi = wi * 8.0;"
// convert back to cartesian coordinates
w.x = wr * sin(wo)*sin(wi);
w.y = wr * cos(wo);
w.z = wr * sin(wo)*cos(wi);
We only have to add c to w now and iterate it in the regular way. You can pretty much then take the code and insert it in your favourite raymarching engine (like this very old but simple one), unless you care about rendering speed.

Optimizing
The above code is mathematically correct, and even fast enough to run in realtime in modern hardware. However, one can still gain a 5x speed factor when rendering in some cases (like when rendering in the CPU in pure C or C++).
The first thing to do is, as usual, to get rid of all those transcendental functions (the trigonometric ones) which not only are slow but also introduce unnecessary errors in the computations. By using the basic trigonometric identities of the cosine and sine of a doubled angle, one can replace the 8-times angle computations by repeatedly applying the identities (three times). The result is a polynomial which has no trigonometric functions and runs much faster in the most CPUs (but not in GPUs usually, which have super fast trigonometric implementations):
float x = w.x; float x2 = x*x; float x4 = x2*x2;
float y = w.y; float y2 = y*y; float y4 = y2*y2;
float z = w.z; float z2 = z*z; float z4 = z2*z2;
float k3 = x2 + z2;
float k2 = inversesqrt( k3*k3*k3*k3*k3*k3*k3 );
float k1 = x4 + y4 + z4 - 6.0*y2*z2 - 6.0*x2*y2 + 2.0*z2*x2;
float k4 = x2 - y2 + z2;
w.x = 64.0*x*y*z*(x2-z2)*k4*(x4-6.0*x2*z2+z4)*k1*k2;
w.y = -16.0*y2*k3*k4*k4 + k1*k1;
w.z = -8.0*y*k4*(x4*x4 - 28.0*x4*x2*z2 + 70.0*x4*z4 - 28.0*x2*z2*z4 + z4*z4)*k1*k2;
You can find a realtime implementation of this here: https://www.shadertoy.com/view/ltfSWn
Coloring
When it comes to rendering, the Mandelbulb can be colored just as any other 3D fractal. Surprisingly nobody that I know out there are coloring 3D fractals so far. Most of them either use a constant color, use the normal to pick a color, or use a random perlin noise pattern to assign a different color to every point in the surface of the set.
In my experiments I opted for using the old orbit traps method applied in 3D but using the results to assign a color. What I did is to compute four orbit traps. One of the traps was the origin, and the other three traps were the x=0, y=0 and z=0 planes. The last three traps were used to mix the basic surface color with three other colors. The point trap in the origin was used as a multiplicative factor to the color, which simulated some ambient occlusion.
The improvement from the other rudimentary coloring methods is that because the behaviour of the orbit traps follows the fractal structure of the set, so do the colors, and therefore we get meaningful color patterns emerging in the surface as opposed to generic perlin noise based coloring.
In my experiments I opted for using the old orbit traps method applied in 3D but using the results to assign a color. What I did is to compute four orbit traps. One of the traps was the origin, and the other three traps were the x=0, y=0 and z=0 planes. The last three traps were used to mix the basic surface color with three other colors. The point trap in the origin was used as a multiplicative factor to the color, which simulated some ambient occlusion.
The improvement from the other rudimentary coloring methods is that because the behaviour of the orbit traps follows the fractal structure of the set, so do the colors, and therefore we get meaningful color patterns emerging in the surface as opposed to generic perlin noise based coloring.
Rendering
Rendering happens as usual, like for any other 3D fractal. My implementation of the Mandelbulb runs realtime in modern GPUs for moderate screen resolutions (say, 720p) with shadows but no antialiasing. It takes a couple of seconds to render in the CPU. To get this speed one has to use distance field based raymarching. In order to generate an SDF out of the fractal, we need a way to approximate the distance to it. At the time when the Mandelbulb was being researched all authors I was aware of were using the wrong distance computation, so I applied first principles and made my own derivations based on the Hubbard-Douady potential theory. Then I applied the usual technique to extract an approximated distance to the surface
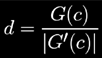
where G(c) is the Hubbard-Douady potential for our polynomial of degree 8:

G'(c) is the gradient of the potential, and can be computer analytically as usual as part of the iteration loop. It can be used also as shading normal once the intersection of the ray with the set is found. This leads to
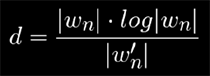
You can find more information about this derivation and how to apply it in the article about distance to fractals.
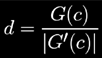
where G(c) is the Hubbard-Douady potential for our polynomial of degree 8:

G'(c) is the gradient of the potential, and can be computer analytically as usual as part of the iteration loop. It can be used also as shading normal once the intersection of the ray with the set is found. This leads to
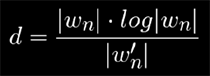
You can find more information about this derivation and how to apply it in the article about distance to fractals.

Orbit trap for coloring. Note that there are no lighting computations of any sort going on
Experiments
The first video is a close zoom to the surface of the fractal object, and the second one is a morphing of the associated Julia sets of the Mandelbulb set.