Intro
Voxels are fun. There's something mesmerizing about their apparence, so it's natural that people use them a lot in their demoscene production, shadertoy creations and even in their visual effects demo reels. Their XYZ plane aligned geometry makes for a good candidate for all sort of rendering optimizations. And also makes it kind of easy to perform some operations that would otherwise be difficult in other contexts. Among such things, there's the computation of shape edges and occupancy.

Voxel edges computed on the fly per pixel (see https://www.shadertoy.com/view/4dfGzs)
Edges
So, you have your voxel volume which is full of either empty or filled cells/voxels, with values 0 or 1 representing the state. You are now shading the face of a voxel cell and you want to mark the pixels belonging to the edges of the voxel shape as such. I will assume that:
- you know if this face is point up, down, left, right, front or back
- you therefore can access the neighbor voxels around this face in "local space"
- you have a vec4 called va with the values of the right, left, front and back side voxels
- you have a vec4 called vb with the values of the front right, front left, back left and back right corner voxels
- you have a vec4 called vc with the values of the right, left, front and back of the voxel above the current
- you have a vec4 called vd with the values of the front right, front left, back left and back right corner voxels of the cell above the current
- you have normalized uv parametrization for the face
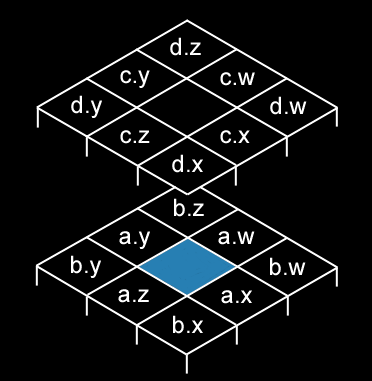
Labeling of the voxel cells involved (in local space)
Now that we have all this information, we can tag the pixels that belong to the edges (within some range in UV space, like 0.85 to 0.95 for example) as actual edges for the voxel solid by looking at the neighbor voxel grid cells stored in va, vb, vc and vd. For example, any of the edges of the blue cell will be an actual geometric edge if the cell to that side va is empty. It will also be an edge if va is not empty but vc, the voxel to the side and above, is also not empty. So, for the right edge of our voxel face we have:
float rightEdge = smoothstep( 0.85, 0.95, uv.x) * ( ((1.0-va.x)||(vc.x))?1.0:0.0 );
We can perform the OR operation above directly with floating point signals by using or(a,b) = a + b - a*b:
float rightEdge = smoothstep( 0.85, 0.95, uv.x) * (1.0-va.x + va.x*vc.x));
We can also do this for the whole four sides of the face at once, if only to bring clarity to the code:
float edges = maxcomp( smoothstep( 0.85, 0.95, vec4(uv.x,1.0-uv.x,uv.y,1.0-uv.y) ) * (1.0-vc*(1.0-va)) );
where maxcomp() returns the largest component of a vector.
This code will work, except that due to the thickness of the edge at rendering time we also need to take care of the corners. We can proceed similarly with the corners though, and flag a corner as belonging to an edge if the vb cell is empty or the vd cell is solid. Putting both edge and corner detectors together produces the following code:
float isEdge( in vec2 uv, vec4 va, vec4 vb, vec4 vc, vec4 vd )
{
// float maxcomp( in vec4 v ) { return max( max(v.x,v.y), max(v.z,v.w) ); }
vec2 st = 1.0 - uv;
// sides
vec4 wb = smoothstep( 0.85, 0.95, vec4(uv.x,
st.x,
uv.y,
st.y) ) * ( 1.0 - va + va*vc) );
// corners
vec4 wc = smoothstep( 0.85, 0.95, vec4(uv.x*uv.y,
st.x*uv.y,
st.x*st.y,
uv.x*st.y) ) * ( 1.0 - vb + vd*vb );
return maxcomp( max(wb,wc) );
}
Fake Occlusion
A very similar technique can be used to compute fake occlusion on the face of a voxel from the immediate neightbor voxels. In this case we only care about the cells above the current cell undergoing shading, vc and vd. For the edges, we can simply use a linear grayscale UV gradient modulated by the neighbor cell occupancy. Or in other words, if the voxel is solid, it produces occlusion. Something like
float rightOcclusion = uv.x * vc.x;
For corners, we want to occlude when the corner cell vd is solid but the edge cells vc are empty, since the case of solid vc cells has already been captured with the previous test. For example, for the front right corner, we'd have
float frontRightOcclusion = uv.x * uv.y * vd.x * (1.0-vc.x)*(1.0-vc.z);
We can put it all together to get
float calcOcc( in vec2 uv, vec4 va, vec4 vb, vec4 vc, vec4 vd )
{
vec2 st = 1.0 - uv;
// edges
vec4 wa = vec4( uv.x, st.x, uv.y, st.y ) * vc;
// corners
vec4 wb = vec4(uv.x*uv.y,
st.x*uv.y,
st.x*st.y,
uv.x*st.y)*vd*(1.0-vc.xzyw)*(1.0-vc.zywx);
return wa.x + wa.y + wa.z + wa.w +
wb.x + wb.y + wb.z + wb.w;
}
which produces kind of decent cheap approximation to short distance occlusion. See the images comparing some simple rendering of a voxel without and with the occlusion approximation enabled:

Ambient + Diffuse lighting

Same as left, with fake occlusion based on neighbor occupancy
There's a live example in Shadertoy of this code (click play to watch it move, or follow https://www.shadertoy.com/view/4dfGzs)